공간 상에서 어느 한 지점의 위치를 정의하기 위해서는 기준이 되는 좌표계(coordinate system)가 필요하다. 그리고 하나의 좌표계는 원점(origin)과 서로 직교하는 세 방향으로 구성된다.
가장 대표적으로 사용되는 좌표계로 직교 좌표계(Cartesian coordinates), 원통 좌표계(cylindrical coordinates) 그리고 구 좌표계(spherical coordinates)가 있다. 어느 좌표계를 사용하는 것이 효과적인가는 정의하고자 하는 물체의 기하학적 형상의 특성에 좌우된다. 예를 들어 지구상의 한 지점의 위치를 정의하기 위해서는 지구의 중심을 원점으로 하는 구 좌표계가 효과적이다.
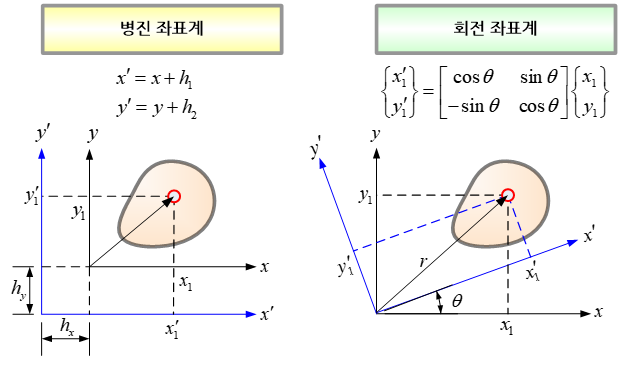
하지만 공학분야에서는 거의 대부분 직교 좌표계를 사용하고 있다. 한 물체 내부에 존재하는 임의 한 지점을 정의하기 위해 하나 이상의 좌표계가 사용될 수도 있다. 이 경우 원점 그리고 직교하는 세 방향은 서로 다르기 때문에 물체 내 동일한 지점에 대해서 두 좌표계에서 서로 다른 좌표값을 가지게 된다. 동일한 위치를 서로 다른 좌표계에서 정의하였을 경우, 한 좌표계에서의 좌표값을 다른 좌표계의 좌표값으로 변환시키는 것을 좌표변환이라고 부른다.
한 물체에 대한 유한요소 해석(finite element analysis)에 있어서도 하나 이상의 좌표계가 사용되는 경우가 빈번하게 발생하기 때문에 좌표변환은 필연적이다. 가장 대표적인 예로서 물체의 기하학적 영역을 세분화한 요소망(mesh) 내 각 유한요소(finite element)의 기하학적 좌표값을 하나의 정규화 된 요소인 마스터 요소(master element)의 좌표값으로 변환하여 각종 행렬(matrix)을 수치적분(numerical integration)하는 경우를 들 수 있다.
.