임의 물체의 거동을 유한요소법(finite element method)으로 근사화시키면 물체의 강성은 강성행렬(stiffness matrix)로 그리고 관성력(inertia force)은 질량행렬(mass matrix)로 표현된다. 그런데 이러한 행렬의 크기는 요소망(mesh)의 크기에 비례하여 증가하기 때문에, 대형 해석문제로 갈수록 행렬이 커져서 컴퓨터에 저장해야 할 행렬요소가 기하급수적으로 증가하게 된다.
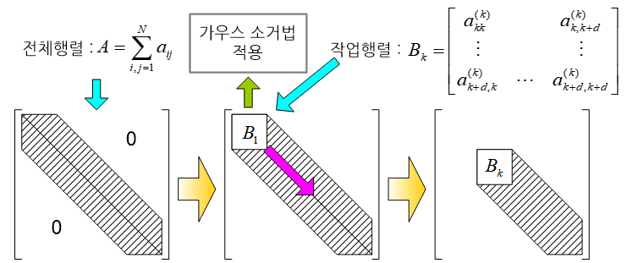
그럼에도 불구하고 일반 개인용 컴퓨터로도 대형 해석문제를 수행할 수 있는 이유는 무엇일까? 그 이유는 유한요소법을 통해 만들어지는 강성행렬과 질량행렬이 띠형상의 분산행렬(banded sparse matrix)이라는 특성때문이다. 행렬의 대각선 주위에만 0이 아닌 행렬요소가 밀집되어 있기 때문에 행렬 전체를 저장하지 않고서도 행렬연산을 수행할 수 있기 때문이다.
이와 같이 행렬 전체를 저장하지 않고 행렬의 대각선을 따라 0인 아닌 행렬의 일부 영역만을 순차적으로 저장해 나가면서 행렬방정식을 풀어나가는 알고리듬이 바로 프론탈 솔버이다. 구조강도 해석과 같은 선형 정적(linear static) 해석은 거의 대부분 이 솔버를 적용하고 있으며, 최근 멀티 프론탈 솔버(multi-frontal solver)와 병렬연산(parallel computing)의 등장으로 저용량 컴퓨터로도 초대형 문제를 아주 빠른 시간내에 해석할 수 있게 되었다.
이 솔버를 프론탈 솔버라고 부르게 된 것은 대각선을 따라 0이 아닌 행렬요소들을 순차적으로 저장하여 풀어나가는 것이 마치 파도가 밀려오는 양상과 흡사하기 때문이다.
.