공기 중을 비행하는 항공기는 주위 공기로부터 압력을 받아 하늘에 떠있을 수 있는 힘을 제공받는 반면, 항공기의 운동은 주변 공기의 흐름에 영향을 미친다. 원유를 수송하는 탱크로리 내부의 원유는 차량의 주행 상태에 따라 출렁임 현상을 나타내고, 이 원유의 출렁임은 다시 차량 전체의 동적인 안정성에 영향을 미친다.
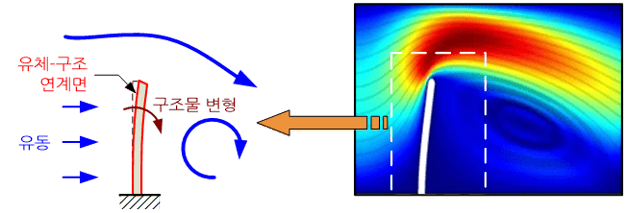
이처럼 우리 주변에는 액체의 흐름과 구조체의 운동(혹은 변형)이 상호 작용을 일으키는 경우가 무수히 많이 존재하고, 이러한 상호작용 문제를 유체-구조 연계문제 혹은 전문용어로 FSI문제라고 부른다. 유체-구조 연계문제에서는 거의 대부분 유체의 흐름에 의해 유발되는 동수압(hydrodynamic pressure)이 접하고 있는 구조체에 하중으로 작용하고, 반면 구조체의 움직임은 유체가 차지하고 있는 기하학적 영역을 변화시킨다. 따라서 유체가 구조물에 미치는 동수압은 구조물에 하중 경계조건(boundary condition)으로 반영되는 반면, 구조물의 거동은 유체 유동의 경계영역 및 경계에서의 속도로 반영된다.
유체-구조물 연계해석에는 다수의 기법들이 적용되고 있는데, 적용하는 수치기법과 좌표계 설정에 따라 기법들이 분류된다. 라그랑지 기술법(Lagrange description)에 기반한 FEM으로 구조물의 변형과 유체의 유동을 연계해서 푸는 방법(coupled FEM-FEM), 구조물의 변형은 라그랑지 기반의 FEM 그리고 유체 유동은 오일러 기술법(Euler description)의 유한체적법(finite volume method)을 혼용하는 푸는 방법(coupled FEM-FVM)이 가장 대표적이다.
유체의 유동이 복잡한 경우 유한요소법을 적용하면 과도하게 뒤틀린 요소(distorted element)가 발생하여 요소망 조정(mesh adaptation, 혹은 remeshing)이 수반되어야 하는 어려움이 존재한다. 그 결과 최근에는 대부분 후자의 방법을 사용하고 있는데, 이 경우에는 유체의 자유표면(free surface)을 파악하기 위한 수치기법이 추가로 필요하다. 유체-구조 연계해석에 있어 꼭 알아야 할 점은 해석결과의 정확도를 높이기 위해 요소크기(element size)를 줄일 경우, 코란트 조건(Courant criterion)을 만족시키기 위해 시간간격(time step)도 동시에 줄어들어야 한다는 점이다.
.