자연현상에 대한 근사적인 답을 구하는 수치해석(numerical analysis)에는 유한요소법(finite element method)이나 유한체적법(finite volume method)을 필두로 매우 다양한 방법들이 존재한다. 종류는 다르지만 모든 수치기법들의 공통된 특징은 정답과의 오차(error)를 최소화 시키고자 하는 것이다. 그런데 이러한 공통점을 지니고 있는 수치기법들이 각기 다른 유형으로 분류되는 근본적인 이유는 근사해(approximate solution)를 구하기 위해 필요한 행렬방정식을 유도하는 방식이 각기 다르기 때문이다.
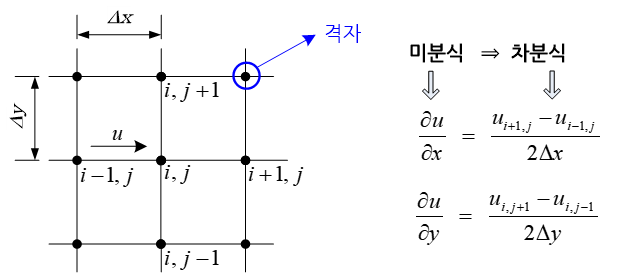
앞서 예를 든 두 기법은 자연현상을 표현하는 수식, 일반적으로 미분방정식 형태의 방정식을 자연현상의 대상이 되는 기하학적 영역에 걸쳐 수치적분(numerical integration)을 취하여 행렬방정식을 유도한다. 하지만 유한차분법은 적분을 취하는 것이 아니라 기하학적 영역 내에 유한개의 점들을 생성하고 서로 이웃하는 점들 사이에서 자연현상의 위치에 따른 변화를 이용하여 비분방정식을 행렬방정식으로 전환시킨다. 기하학적 영역 안에 생성된 유한개의 점들을 격자(grid)라고 부르고 격자의 조밀도에 따라 근사해의 정확도는 증가한다.
유한차분법은 상대적으로 적용이 용이하기 때문에 학술적인 연구나 간단히 해답을 구하고자 할 경우에 매우 효과적이다. 하지만 대상이 되는 물체의 형상이 복잡해 질수록 각 좌표축 방향으로의 변화율을 정의하기가 어렵게 되기 때문에 일반화 시키기가 쉽지 않은 단점을 지니고 있다.
.