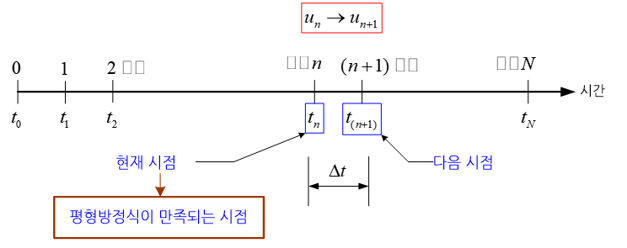
시간에 따라 변하는 물체의 거동을 수치해석을 통해 구하는 경우, 시간 구간을 다수의 시점으로 나누어 각 시점에 해당하는 거동값을 순차적으로 계산하는 시간적분 기법의 하나이다. 각 시점에서의 물체의 거동은 주어진 초기조건(initial condition)을 이용하여 다음 시점에서의 거동값을 계산하고, 계산된 값을 이용하여 그 다음 시점에서의 거동값을 계산하는 방식으로 순차적으로 구해진다. 이렇게 순차적으로 시간에 다른 물체의 거동을 계산하는 것을 시간적분(time integration)이라고 부른다.
시간에 따라 변하는 물체의 거동을 표현하는 수학식에는 시간에 따른 변화율이 포함되어 있기 때문에, 그 해답을 구하기 위해서는 이론적으로 시간에 대해 적분을 수행하여야 한다. 이러한 맥락에서 시간적분이라는 단어를 사용하게 되었다. 명시적 시간적분은 다음 시점에서의 거동값을 계산하기 위해 거동에 대한 수학적 표현식을 이전 시점인 현 시점에 놓고 푸는 방법이다. 현 시점에서의 거동값은 이미 계산되어 아는 값이기 때문에 암시적 시간적분(implicit time integration)보다 계산과정이 매우 간단하다.
이 시간적분은 물체의 관성력과 관련이 있는 질량행렬(mass matrix)의 행렬 대각화(matric diagonalization)와 병행하여 사용되는 것이 일반적이다. 왜냐하면 거대한 크기의 행렬방정식을 푸는데 걸리는 시간을 현저하게 줄여주기 때문이다. 다라서 암시적 시간적분에 비해 계산시간이 단축되기 때문에 대형 해석문제를 푸는데 적합하고, 최근 해석문제의 대형화에 따라 거위 대부분 시간적분은 이 기법으로 처리되고 있다.
하지만 이 기법은 요소 크기(element size)와 시간 간격(time step)이 코란트 조건(Corant condition)이라는 특정한 조건식을 만족하지 않으면 해석결과가 수렴(converge)하지 않거나, 정확도가 낮은 해석결과를 제공하는 취약점이 있다.
.