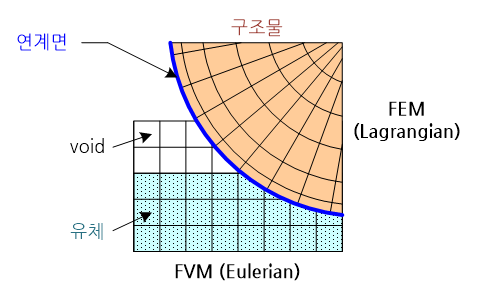
유체와 구조물이 접촉하고 있는 경우 유체의 유동과 구조물의 변형(deformation)은 두 매질의 공통경계(common interface)를 통하여 상호 영향을 미친다. 이러한 유체-구조 연계해석(fluid-structure interaction analysis)에 있어 구조물은 라그랑지 기술법(Lagrange description)의 유한요소법을 그리고 유체 영역은 오일러 기술법(Euler description)의 유한체적법(finite volume method)을 주로 사용하고 있다.
그 주된 이유는 구조물은 연속체(continuum body)로써 변형의 정도가 유체에 비하여 비교가 되지 않을 정도로 작아서 변형에 따른 요소망(mesh)의 찌그러짐이 그다지 문제가 되지 않는다. 하지만, 유체는 흐름이 매우 복잡하고 혼동스럽기 때문에 라그랑지 기반의 요소망을 적용하게 되면 요소의 찌그러짐이 큰 문제로 대두된다. 따라서 유체 영역은 유체의 흐름과는 무관하게 항상 공간상에 고정된 오일러 기반의 격자를 적용하게 된다.
이와 같이 움직이는 요소망과 공간상에 고정된 격자 사이 공통경계에서, 요소망과 격자의 분포가 정확히 일치하지 않는 경우에 유체의 압력과 구조물의 변형을 서로 주고 받기 위한 연계처리기법이 바로 오일러-라그랑지 연계법이다. 이 기법은 에이엘이 연계법(ALE coupling)과는 달리 두 매질이 접촉하고 있는 공통경계의 기하학적 형상이 복잡한 경우에 매우 효과적이다.
그 이유는 구조물의 요소망과 유체의 격자 중에서 조밀한 경계면을 단순히 연계요소망(coupling mesh)로 정의하기만 하면 되기 때문이다. 이러한 장점 때문에 거의 대부분의 유체-구조 연계해석에서는 이 연계법을 적용하고 있다. 그 대표적인 경우로 자동차 타이어의 수막현상(hydroplaning) 그리고 선박의 유탄성(hydroelasticity) 해석을 들 수 있다.
.