보 형상의 가느다란 부재의 역학적 거동을 많은 가정을 통하여 가장 단순하게 수학적으로 표현한 오일러 보 이론(Euler beam theory)을 토대로 하는 1차원 보 요소(beam element)이다. 오일러 보 이론은 18세기 스위스의 위대한 수학자인 오일러(1707~1783)와 그의 스승 베르누이(Bernolli)에 의하여 탄생하였다.
이 이론에서는 보 형상 구조물의 처짐(deflection)은 외부에서 가한 일과 구조물 내부에 저장되는 굽힘 변형에너지는 같다는 원리로부터 유도된다. 하지만 구조물의 횡 전단 변형에너지는 무시되기 때문에 구조물의 두께가 길이에 비해 현저히 작지 않은 경우에는 정확도가 떨어지는 단점이 있다. 하지만 오일러 보 이론은 이론적인 해답을 제공하기 때문에 공학분야에서 직면하는 많은 보 구조물의 처짐량을 계산할 때 참고가 되는 해를 제공해 준다.
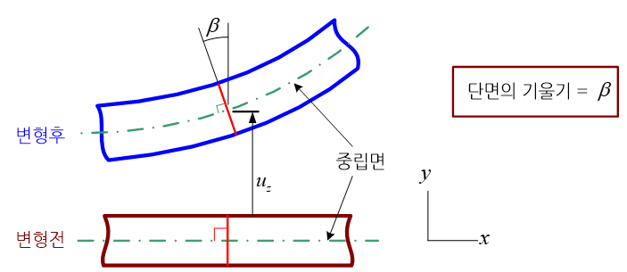
오일러 보 이론에서는 보의 처짐이 4차 미분방정식으로 표현되고, 이것을 유한요소(finite element)로 구현하기 위해서 한 절점이 가져야 할 자유도(degree of freedom)는 구조물의 처짐과 처짐의 기울기이다. 참고로 이 이론은 그 이후 러시아의 공학자인 티모센코(Timoshenko)에 의하여 개선되었으며, 이 개선된 보 이론을 티모센코 보(Timoshenko beam) 이론이라고 부른다.
.