하중을 받는 물체의 항복 혹은 파괴를 예측하기 위한 이론들 중에서 트레스카 항복조건(Tresca yield criterion)과 쿨롱-모어 이론(Coulomb-Mohr theory)은 주응력(principal stress)을 좌표축으로 하는 3차원 공간상에서 육면체의 다각형으로 표현된다. 그 이유는 이들 이론들이 물체 내 전단응력을 파괴 예측의 기준으로 삼고 있기 때문이다. 이들 이론들은 다각형의 각 면이 직선으로 표현되기 때문에 이론식으로 표현하기가 쉽다.
하지만 이 모서리부로 인해 이들 이론들을 수치해석(numerical analysis)에 적용할 때 많은 어려움을 안겨준다. 왜냐하면 다각형 형상의 항복기준에 있어 항복이 발생하기 쉬운 방향을 나타내는 법선벡터(normal vector)가 모서리 부분에서 갑자기 변함으로 인해 불연속이 되기 때문이다. 수치해석에 있어서 이러한 단위벡터의 불연속은 항복곡면을 수치해석적으로 처리하는 과정에서 많은 문제점을 야기한다.
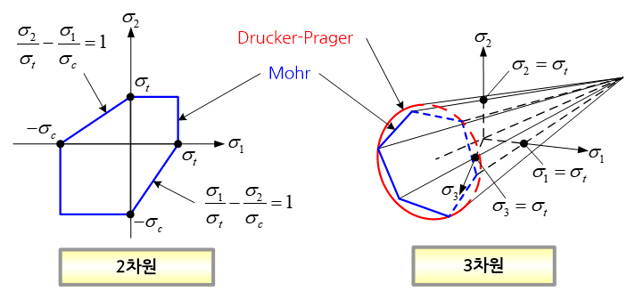
따라서 이러한 문제를 해결할 수 있는 이론이 바로 드러커-프라거 항복기준이다. 이 이론은 최대 비틀림 에너지를 항복예측의 기준으로 삼는 폰-미제스 항복기준(von-Mises yield criterion)을 토양이나 눈과 같은 물질로 확장시킨 것이다. 이 이론은 주응력을 좌표축으로 하는 3차원 공간상에 나타내면 타원형으로 표현될뿐더러, 쿨롱-모어 이론의 기하학적 형상의 외접 타원형이 되기 때문에, 쿨롱-모어 이론보다 물체가 파괴되지 않고 안전한 범위가 넓은 특징을 지니고 있다.
.