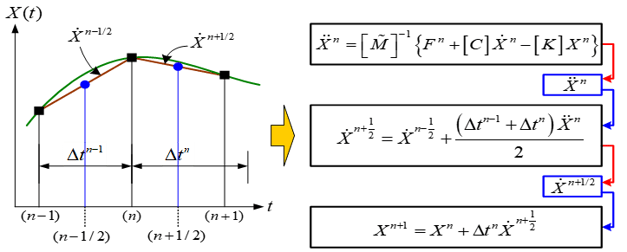
시간에 따라 변하는 물체의 응답을 수치해석(numerical analysis)을 통해 구하기 위해서는, 관찰 대상이 되는 시간 구간을 유한 개의 시점으로 나누고 각 시점에서의 거동을 순차적으로 계산해 나간다. 다시 말해, 초기조건(initial condition)을 이용하여 다음 시점에서의 응답을 계산하고 계산된 이 응답을 이용하여 그 다음 시점에서의 응답을 계산하는 순차적인 반복계산으로 관찰 대상구간 내 응답을 계산하게 된다.
이와 같이 시간에 따른 응답을 유한 개의 시점으로 나누어 순차적으로 응답을 구하는 것을 시간적분(time integration)이라고 부른다. 이러한 시간적분에는 크게 명시적 시간적분(explicit time integration)과 암시적 시간적분(implicit time integration) 으로 나뉘며, 중앙차분법은 대표적인 명시적 시간적분 기법이다.
이 기법에서는 현시점에서의 가속도를 이전 시점과의 중앙시점 그리고 다음 시점과의 중앙시점에서의 속도 두 개를 이용하여 근사적으로 구한다. 그런 다음, 다음 시점과의 중앙 시점에서의 속도를 근사적으로 구하고, 최종적으로 다음 시점에서의 물체의 응답을 근사적으로 계산하게 된다. 이러한 계산방법을 시점에 따라 순차적으로 적용하게 되면 관찰 대상구간에서의 모든 시간 응답을 근사적으로 구할 수 있게 된다.
이 기법은 시간에 따라 변하는 물체의 거동뿐만 아니라 공간상에서 변하는 물체의 거동, 즉 변화율을 가지는 미분 문제에도 많이 사용되고 있다. 이 기법은 해의 안정성(stability of solution)과 해의 수렴성(convergence of solution)을 모두 만족시킬 뿐만 아니라 정확성이 높다는 장점을 지니고 있다.
.