하중을 받으면 물체는 변형되고 물체의 내부에는 외력에 저항하려는 내력 즉, 응력(stress)이 발생하게 된다. 지구 상의 대부분의 물체는 연속적이고 조밀한 분포를 가진 입자들로 구성되어 있다. 이러한 측면에서 연속체(continuum material)라는 용어를 사용하고 있으며, 변형이나 응력과 같은 물체의 거동은 물체 내에서 연속적인 분포를 나타낸다.
그런데 이러한 물체의 거동을 유한요소해석(finite element analysis)과 같은 수치기법으로 근사해(approximate solution)를 구하게 되면 변형은 연속적인 분포를 나타내지만, 변형률(strain)과 응력은 요소망(mesh) 내 이웃한 유한요소(finite element) 사이에서 불연속성을 나타낸다. 그 이유는 다름아닌 물체의 변형을 근사화 하기 위해 사용되는 보간함수(interpolation function, 혹은 기저함수(basis function)라고도 불림)의 특성 때문이다.
유한요소해석에 사용되는 대부분의 보간함수는 기본적으로 인접한 요소 사이에서 연속적이지만 이 함수의 미분은 요소 사이에서 불연속적이다. 변형률과 응력은 모두 변형의 미분으로 정의되기 때문에 결국 변형률과 응력은 인접한 요소 사이에서 불연속적인 분포를 나타내게 되는 것이다. 하지만 우리가 상용 유한요소해석 프로그램을 사용하여 화면상에 응력을 출력하면 인접한 요소 사이에서 연속적인 분포를 보여준다. 이것은 프로그램 내에서 불연속적인 변형률과 응력을 연속적인 분포를 갖도록 인위적으로 수정하기 때문이다.
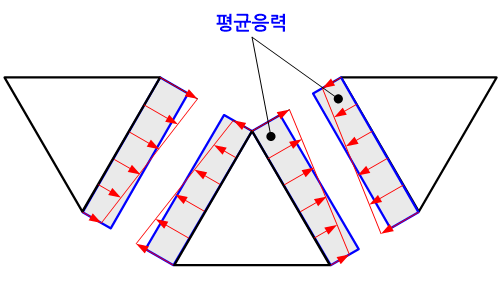
대부분의 경우 인접한 요소들의 공동 경계면(interface)에서의 변형률 혹은 응력값의 평균을 취하여 연속적인 분포로 수정하고 있다. 이처럼 인접한 요소 사이에서 불연속한 응력값의 평균을 취하여 정의한 응력을 평균응력이라고 부른다.
.