외부로부터 동적인 하중(dynamic load)을 받는 물체는 시간에 따라 변화하는 동적 거동을 나타낸다. 그리고 이러한 동적 거동에 대한 해답을 찾아내는 작업을 동해석(dynamic analysis)이라고 부른다. 특히 유한요소법(finite element method)과 같은 수치해석에서는 이러한 동해석은 동적거동을 수학적으로 표현한 미분방정식을 시간적으로 적분하여 근사해(approximate solution)를 구한다.
관심이 되는 시간 영역을 유한 개의 시점으로 나누고, 각 시점에서 물체의 거동을 초기조건(initial condition)을 이용하여 순차적으로 풀어나가게 된다. 그리고 이러한 작업을 시간적분(time integration)이라고 부르는데, 이러한 수치적 적분을 통해 구한 물체의 시간응답은 정답과는 달리 예상치 않은 요동(oscillation), 불안정성(instability) 그리고 발산(divergence) 등과 같은 문제점을 나타낸다. 이러한 문제점은 수치적인 시간적분이 안고 있는 본질적인 결함으로써, 이것을 최소화 시키기 위해 여러가지 기법들이 소개되어 있다.
예를 들어, 시점과 시점 사이의 간격, 즉 시간간격(time step)의 크기나 요소크기(mesh size)를 줄이는 것이 가장 대표적인 방안이다. 특히, 물체가 지니고 있는 감쇠(damping)를 무시하고 동해석을 수행하는 경우에는 이러한 문제점이 두드러지며, 시간간격과 요소크기를 줄이는 것만으로는 문제를 해결할 수 없는 경우가 종종 발생한다. 특히 과도응답(transient response)이 지배적인 문제에서는 특히 어려움이 많다.
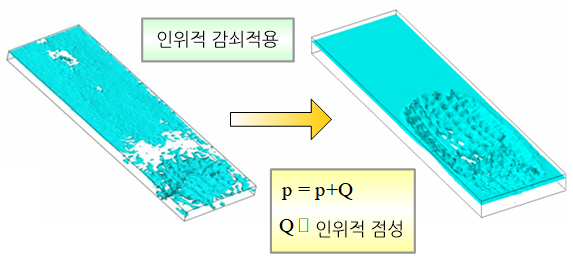
이와 같이 물체가 지니고 있는 감쇠를 무시한 동해석에 있어 시간응답 상의 요동, 불안정성, 발산 등을 억제하기 위해 사용되는 기법이 바로 인위적으로 감쇠를 부과하는 것이다. 이 기법은 요소망(mesh) 전체 혹은 부분적인 영역에 인위적으로 감쇠를 부여하는 것으로, 부과하게 되는 감쇠값을 결정하는 방법에는 여러가지 방법들이 소개되어 있다.
.