유한요소해석(finite element analysis)을 통해 임의 물체의 거동을 분석하는 경우, 구하게 되는 근사해(approximate)의 정확도가 원하는 수준에 미치지 못하는 경우가 많다. 근사해의 정확도는 오차평가(error estimate)라 불리는 특별한 기법이나 이론적인 정답 혹은 실험결과와의 비교 등을 통하여 수행된다.
그리고 근사해의 정확도는 요소망(mesh)의 조밀도 혹은 유한요소(finite element)에 적용되는 기저함수(interpolation function)의 차수 그리고 입력 값으로 입력되는 재료 물성치(material properties), 경계조건(boundary condition), 그리고 수치기법과 관련된 각종 수치 파라메터(parameter)에 의하여 좌우된다.
적응적 유한요소 해석이란 원하는 정확도를 만족하는 근사해를 구하기 위하여 이러한 값들을 조절하면서 오차(error)를 줄여가는 일종의 반복해석 과정을 말한다. 흔히 요소망의 밀도와 기저함수의 차수를 조정하게 되는데, 보다 합리적으로 조정하기 위하여 선 오차평가(a priori error estimate)와 후 오차평가(a posteriori error estimate)를 동시에 활용한다.
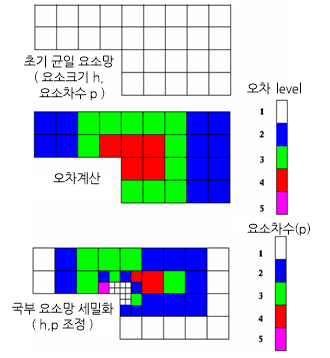
적응적 유한요소해석의 절차는 다음과 같이 구성된다. 우선 해석자가 초기에 설정한 요소망과 기저함수의 차수로 유한요소 해석을 수행하고, 해석결과의 정확성을 후 오차평가를 통하여 정량적으로 계산한다. 이렇게 계산된 오차값을 선 오차평가에 대입하여 원하는 정확도를 만족시킬 수 있는 유한요소의 크기(h)와 기저함수의 차수(p)를 계산한다.
계산된 유한요소의 크기와 기저함수의 차수를 적용하여 요소망을 세밀화(mesh refinement)한 다음 유한요소 해석을 재차 수행한다. 그리고 해석결과에 대한 정확도를 후 오차평가를 이용하여 재차 계산한다. 만일 여전히 원하는 정확도에 미치지 못하면 이러한 과정을 반복한다.
.